e
q
u
e
s
t
a
d
e
m
o
Algorithms
{TOC}
Substitution
Substitution masks data by replacing a given value with another value suitable for the given entity, be it a field or part of the text or any other type of an entity. Substitution could be random or pseudo-random, could preserve referential integrity and statistical distribution or disturb it, and could deal with the whole, at-once, value replacements or complex replacement patterns of the parts of the entity.
In mathematical terms, the substitution method of data masking allows mapping of members of one set to the members of another set, such that the members of replacing set are of the same intensional definition.
Random
Random substitution masks data by replacing a given value with a random value from a pre-compiled data set. Values in the data set are suitable and conform to the same rules or definitions that of the given value. With each iteration of the masking algorithm, another random value gets chosen and replaces the value on the input. An example would be a value of John being masked with values of Alex, Robert, and Mike in subsequent iterations of the substitution operation.
As data masking of the given value with Random Substitution does not guarantee to be repeatable among cycles, it is not suitable for masking data sets with unique constraints and requires extra work of preserving referential integrity if used on the values of fields preserving referential integrity constraint. In denormalized data sets it might cause difficulties in implementing row-internal synchronization, table internal synchronization and table-to-table synchronization operations.
Preserving Referential Integrity
These are algorithms that mask data by replacing a given value with a pseudo-random value from a pre-compiled data set. The "pseudo" comes from the fact that there is an underlying algorithm that matches a given value to the very same value at each iteration of the substitution operation.
An example would be a value of a name Jane always masked with the value of the name Virginia. Such substitution allows for better preservation of referential integrity as well as for synchronization of values among cells in the same and different tables and in the text.
Replacing sets in the substitution data masking algorithm could have the same numbers of values as original sets ( the same cardinality) or different number of values.
Disturbing Statistics
For certain types of de-identified data, its statistics becomes security's "enemy". Such examples were identified by Dr. Latanya Sweeney , then graduate student, today's Harvard's professor with specialization in computer science and privacy. She identified such data and HIPAA's famous 18 elements list some of them: zip codes, dates of births, as well as the rules that allow to change this statistics. When a subtype of substitution data masking technique matches data sets with the same cardinality (the same number of elements), one to one, the statistical distribution of the resulting set values is completely preserved. If there exists a public data set and/or its statics is in the public domain, someone knowing the statistics could re-identify the de-identified data. An example of such risk is explained in the webinar. You could also see how easy/hard it is to find out the risk of identifying you statistically : How Unique Are You? Thus, it is important to make sure that "statistics" is disturbed, by changing set cardinalities or providing the algorithms that change statistical distributions ( patent pending).
Unique
Some of the data is designed to be unique. Its statistical value is insignificant in the paradigm of the re-identification risks.
The representative elements of such data are those that have one value per person or household: social security, passport, credit card, and phone numbers are prime examples.
They are unique within the context. As such, it is important often in code to replace them with other unique values of the same format, but not belonging to that particular person.
E.g. American phone number shell retain one of the formats defined by North American Numbering Plan (NANP), such as xxx- xxx-xxxx or +1 (xxx) xxx xx xx
For de-identifying the unique elements, several methods are used, including unique substitution, shuffling, and format preserving encryption.
Character Permutation and Character Substitution
Two algorithms that manipulate character of a given string.
The character permutation data masking algorithm uses characters of a given string as an input set and maps this set on itself by creating various permutations of the characters of the string either randomly or in pre-defined repeatable pattern.
The character substitution data masking algorithm, besides given string value, uses another set of the characters with the specific mapping rules, creating an output based on either random or predefined mappings.
The strongest masking algorithm of this variety is random character substitution, followed by random character permutation and pre-defined character substitution, followed by pre-defined character permutation.
Format Preserving Encryption
FPE was developed by Voltage and is a form of encryption that preserves format. It is not per se "data masking" as potentially the value can be decrypted, however it is a convenient format for tokenization.
Shuffle
Shuffle is a data masking algorithm that allows to preserve all the values in the given column as they were while it changes the position of the value(s) in the column comparing with their initial position. The name reflects a "shuffling" action. The algorithm is useful when it is necessary to preserve the aggregated values and it could be used for columns with unique constraint. As an example, let's consider a column with sales numbers - if the resulting quarterly sales need to remain intact so that not to break an application, we would want to use a shuffling algorithm.
Date Variance
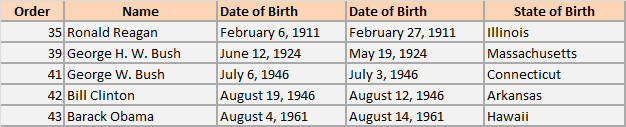
When one anonymizes data, one needs to make precautions that anonymization is, indeed, a one-way road. It is hard to accomplish with dates for at least two reasons. Dates are often used as query parameters in reports and from the business perspective, when one searches on a date, the date range should be determined, for testing. Second, ages and dates of births distributions are necessary elements in both medical and financial statistics. Thus, they are not only used for searching, they are elements of the resulting reports. Adding or subtracting a preset same number of days from all the date values in the column is easily decodable. In order to anonymize the data properly, yet allowing for the aggregate values to be within specific range, one would want to define a special interval within each to change values. Such an algorithm is called date variance. For example, one would want to change all the dates of birth within a month of the original date of birth. Note: it is important to change dates of birth of people who are older than 89 years old in such a way that they do not cross 89 years old threshold, as at this point the demographics statistics allows guessing the person easily. Read more about limits of dates values here. Examples of the data variance algorithm application you can see in the picture depicting the dates of births of the latest presidents of United States, their real value and the masked value within a month range of the original date.
Number Variance
Similar to dates, changing value of an integer is challenge in proper data anonymization. Adding or subtracting the same value to the, for example, sales per months, is easy to re-identify if a person knows at least some of the sales figures. Thus, what's needed is to allow adding/subtracting value to the original value within a specific predefined interval. For example, adding or subtracting values to sales that allow to keep let's say, normal distribution with its original deviation, such as its confidence interval, etc.
Nulling
This is the simplest algorithm of all that requires no specific knowledge or tools. All the values are replaced by nulls. It is also the most secure algorithm. However, while secure, it is often the one that breaks application logic the most. As a result, it is the one to use with caution.
Mask A Key
Key masking is a deterministic form of data masking that creates a seed value for the element being masked. This limits the masking output to certain characters of the same seed value to retain referential integrity.
Mask Redaction
The Mask redaction component redacts data character per character with the character defined in the custom properties. It can be “*”,”x”,”+”,” “ or any other character. It is a very simple component gear towards complete value redaction.
Number Rollup
A number rollup algorithm is a form of generalization that allows a user to set a range of numerical values for the input of numerical data in order to ensure a generalized value will be outputted.
